Model selection using refnx and dynesty
refnx + dynesty can be used to obtain the Bayesian evidence, which allows you to perform model selection.
[1]:
%matplotlib inline
import numpy as np
import dynesty
from refnx.analysis import Objective, Model, Parameter, Parameters
from refnx.dataset import Data1D
import matplotlib.pyplot as plt
[2]:
def gauss(x, p):
A, loc, sd = p
y = A * np.exp(-((x - loc) / sd)**2)
return y
We’ll synthesise some experimental data from two Gaussians with a linear background. We’ll also add on some noise.
[3]:
x = np.linspace(3, 7, 250)
rng = np.random.default_rng(0)
y = 4 + 10 * x + gauss(x, [200, 5, 0.5]) + gauss(x, [60, 5.8, 0.2])
dy = np.sqrt(y)
y += dy * rng.normal(size=np.size(y))
data = Data1D((x, y, dy))
[4]:
data.plot();

[5]:
# this is our model that we want to fit.
# It will have a linear background and a number of Gaussian peaks
# The parameters for the background and each of the Gaussian peaks
# will be held in separate entries in `p`.
def n_gauss(x, p):
y = np.zeros_like(x)
# background parameters
a, b = np.array(p[0])
y += a + b*x
for i in range(1, len(p)):
g_pars = p[i]
A, loc, sd = np.array(g_pars)
y += gauss(x, [A, loc, sd])
return y
[6]:
# the overall parameter set
pars = Parameters(name="overall_parameters")
# parameters for the background
bkg_pars = Parameters(name='bkg')
intercept = Parameter(1, name='intercept', bounds=(0, 200), vary=True)
gradient = Parameter(1, name='gradient', bounds=(-20, 250), vary=True)
bkg_pars.extend([intercept, gradient])
pars.append(bkg_pars)
# now go through and add in gaussian peaks and calculate the log-evidence
model = Model(pars, n_gauss)
logz = []
for i in range(4):
if i:
A = Parameter(5, name=f"A{i}", bounds=(40, 250), vary=True)
loc = Parameter(5, name=f"loc{i}", bounds=(3, 7), vary=True)
sd = Parameter(5, name=f"sd{i}", bounds=(0.1, 2), vary=True)
g_pars = Parameters(data=[A, loc, sd], name=f"gauss{i}")
pars.append(g_pars)
objective = Objective(model, data)
nested_sampler = dynesty.NestedSampler(
objective.logl,
objective.prior_transform,
ndim=len(pars.varying_parameters())
)
nested_sampler.run_nested()
logz.append(nested_sampler.results.logz[-1])
5907it [00:05, 1075.69it/s, +500 | bound: 14 | nc: 1 | ncall: 28160 | eff(%): 22.752 | loglstar: -inf < -4233.325 < inf | logz: -4244.268 +/- 0.198 | dlogz: 0.001 > 0.509]
12557it [00:18, 696.48it/s, +500 | bound: 48 | nc: 1 | ncall: 53297 | eff(%): 24.499 | loglstar: -inf < -1048.585 < inf | logz: -1072.989 +/- 0.313 | dlogz: 0.001 > 0.509]
17403it [11:47, 24.60it/s, +500 | bound: 2186 | nc: 1 | ncall: 1701762 | eff(%): 1.052 | loglstar: -inf < -913.031 < inf | logz: -947.230 +/- 0.372 | dlogz: 0.001 > 0.509]
19222it [02:40, 119.67it/s, +500 | bound: 261 | nc: 1 | ncall: 461894 | eff(%): 4.270 | loglstar: -inf < -911.813 < inf | logz: -949.640 +/- 0.392 | dlogz: 0.001 > 0.509]
[7]:
print(logz)
[-4244.267669942061, -1072.989448001302, -947.2295781758878, -949.6400447012933]
[8]:
plt.plot(logz)
[8]:
[<matplotlib.lines.Line2D at 0x7fbe3bd87130>]
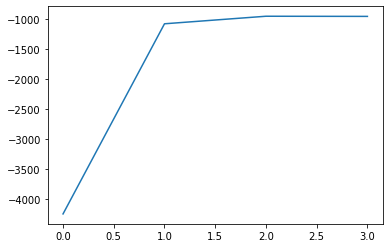
The log-evidence points to the use of 2 Gaussians to fit the data. There is a sufficient increase in evidence over 1 Gaussian. However, 3 Gaussians is not justified, the logz term does not increase.
[ ]: